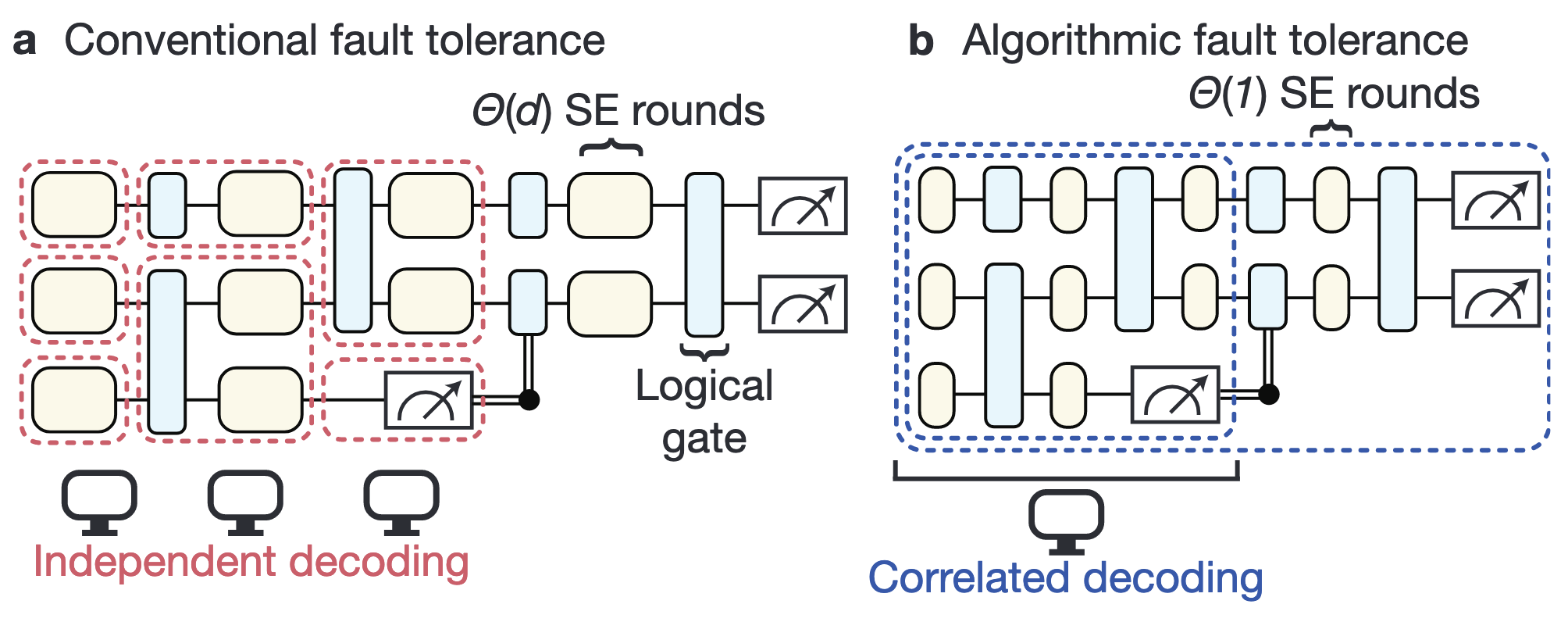
Fast, reliable logical operations are essential for realizing useful quantum computers. By redundantly encoding logical qubits into many physical qubits and using syndrome measurements to detect and correct errors, we can achieve low logical error rates. However, for many practical quantum error correction codes such as the surface code, owing to syndrome measurement errors, standard constructions require multiple extraction rounds—of the order of the code distance d—for fault-tolerant computation, particularly considering fault-tolerant state preparation. Here we show that logical operations can be performed fault-tolerantly with only a constant number of extraction rounds for a broad class of quantum error correction codes, including the surface code with magic state inputs and feedforward, to achieve ‘transversal algorithmic fault tolerance’. Through the combination of transversal operations and new strategies for correlated decoding13, despite only having access to partial syndrome information, we prove that the deviation from the ideal logical measurement distribution can be made exponentially small in the distance, even if the instantaneous quantum state cannot be made close to a logical codeword because of measurement errors. We supplement this proof with circuit-level simulations in a range of relevant settings, demonstrating the fault tolerance and competitive performance of our approach. Our work sheds new light on the theory of quantum fault tolerance and has the potential to reduce the space–time cost of practical fault-tolerant quantum computation by over an order of magnitude.