Publications RSS feed
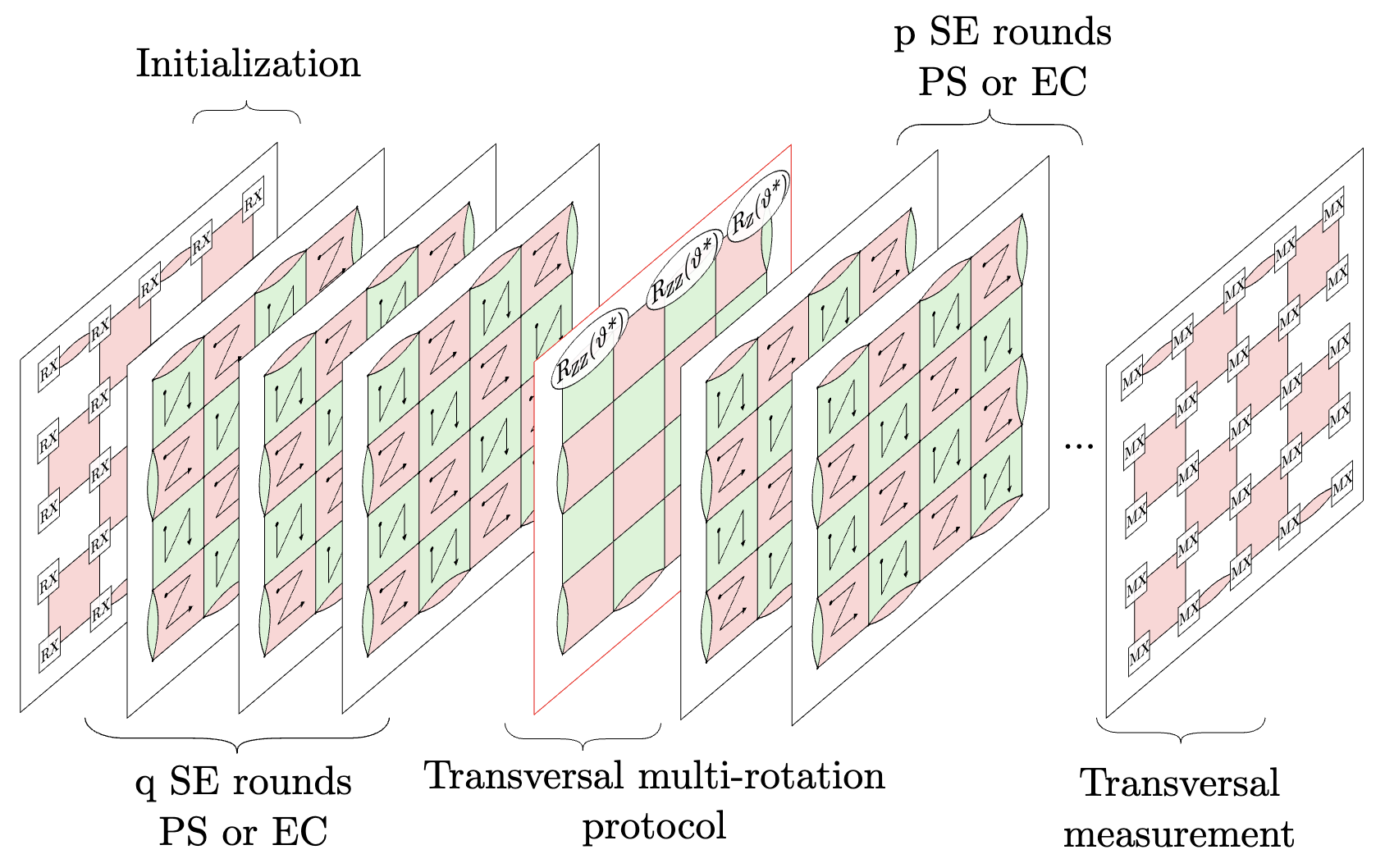
- Transversal STAR architecture for megaquop-scale quantum simulation with neutral atoms
Abstract
Quantum computing experiments have made remarkable progress in demonstrating key components of quantum error correction, a prerequisite for scalable quantum computation. While we anticipate the arrival of early fault-tolerant quantum hardware capable of a million reliable quantum operations, the cost of preparing low-noise `magic resource states' presents a formidable challenge. The recently proposed partially-fault-tolerant architecture based on a space-time efficient analog rotation (STAR) approach attempts to address this challenge by using post-selection to prepare low-noise, small-angle magic states. Its proposed physical implementation, however, assumes fixed qubit connectivity, resulting in implementation costs closer to leading fully-fault-tolerant approaches. Here, we propose the transversal STAR architecture and co-design it with neutral-atom quantum hardware, deriving significant savings in logical layout, time, and space overhead. Through circuit-level simulations, we derive the logical noise model for surface-code-based transversal STAR gadgets and verify their composability. At its limit, the transversal STAR architecture can efficiently simulate local Hamiltonians with a total simulation volume exceeding 600. Achieving this limit would require approximately 10,000 physical qubits at a physical error rate of 10−3. This is equivalent to a fully-fault-tolerant computation requiring over 106-107 T gates. Finally, we extend the transversal STAR architecture to high-rate quantum codes, demonstrating how a limited set of highly parallel transversal Clifford gates and generalized small-angle magic injection can be utilized for effective quantum simulation. We anticipate that the co-designed transversal STAR architecture could substantially reduce the physical resources necessary for early-fault-tolerant quantum simulation at the megaquop scale.
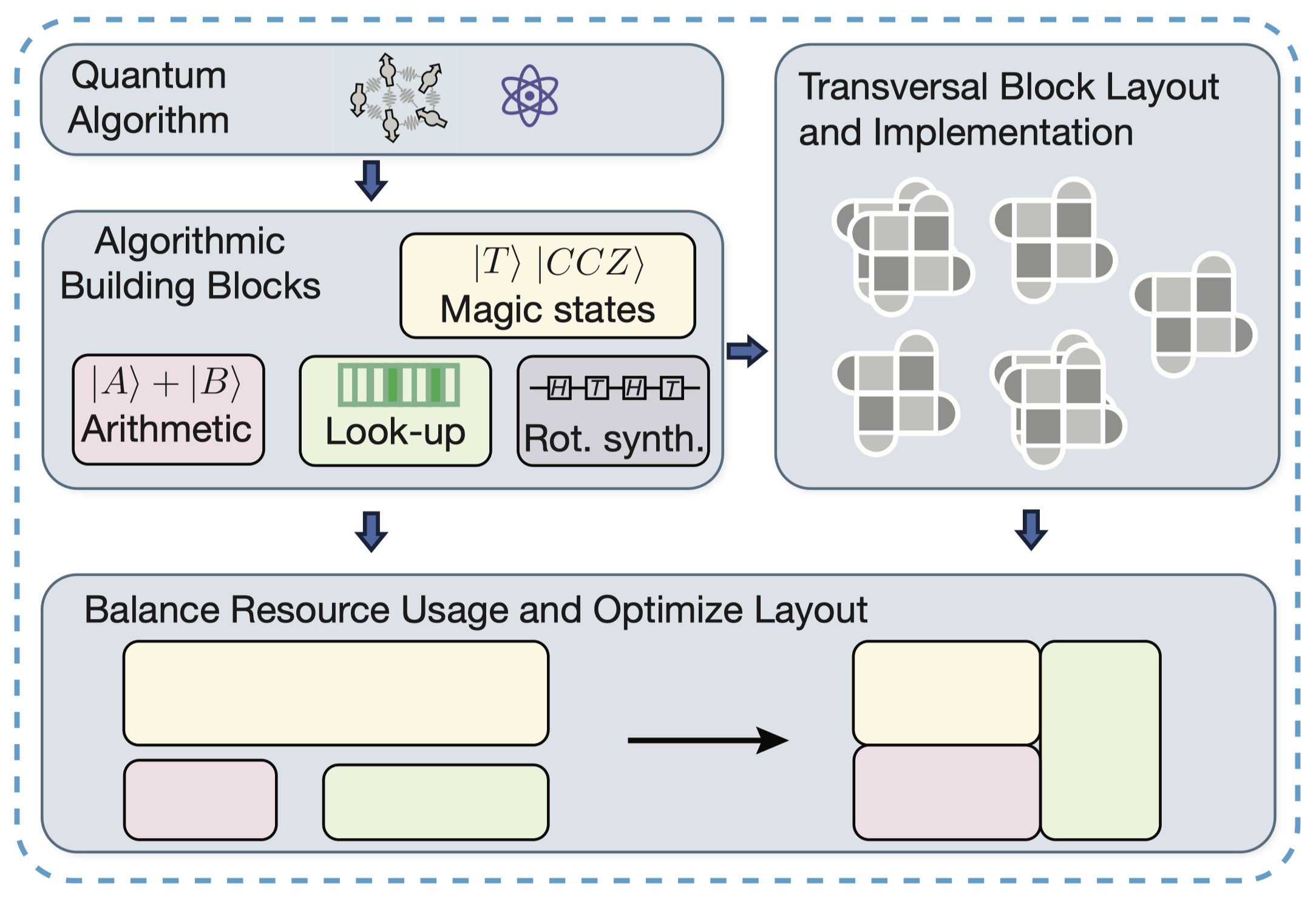
- Resource Analysis of Low-Overhead Transversal Architectures for Reconfigurable Atom Arrays
Abstract
Neutral atom arrays have recently emerged as a promising platform for fault-tolerant quantum computing. Based on these advances, including dynamically-reconfigurable connectivity and fast transversal operations, we present a low-overhead architecture that supports the layout and resource estimation of large-scale fault-tolerant quantum algorithms. Utilizing recent advances in fault tolerance with transversal gate operations, this architecture achieves a run time speed-up on the order of the code distance d, which we find directly translates to run time improvements of large-scale quantum algorithms. Our architecture consists of functional building blocks of key algorithmic subroutines, including magic state factories, quantum arithmetic units, and quantum look-up tables. These building blocks are implemented using efficient transversal operations, and we design space-time efficient versions of them that minimize interaction distance, thereby reducing atom move times and minimizing the volume for correlated decoding. We further propose models to estimate their logical error performance. We perform resource estimation for a large-scale implementation of Shor’s factoring algorithm, one of the prototypical benchmarks for large-scale quantum algorithms, finding that 2048-bit RSA factoring can be executed with 19 million qubits in 5.6 days, for 1 ms QEC cycle times. This represents close to 50× speed-up of the run-time compared to existing estimates with similar assumptions, with no increase in space footprint.
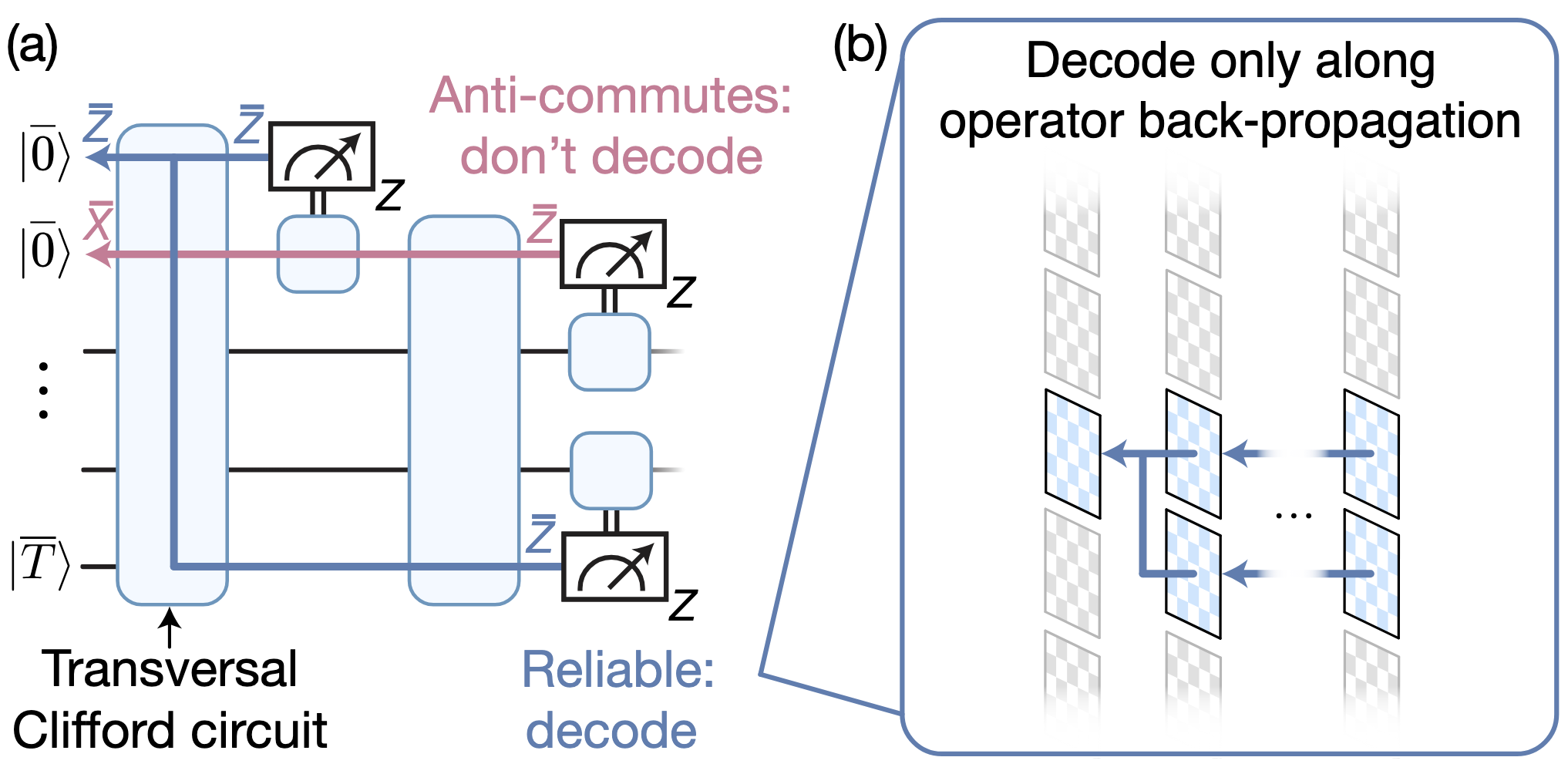
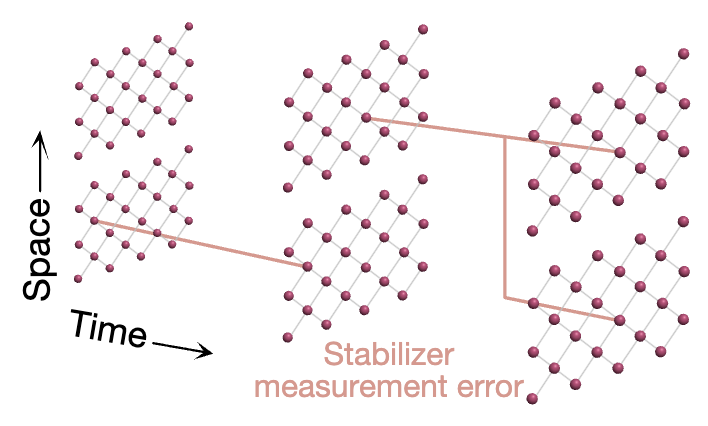
InISCA '25: Proceedings of the 52nd Annual International Symposium on Computer Architecture - Fast correlated decoding of transversal logical algorithms
Abstract
Quantum error correction (QEC) is required for large-scale computation, but incurs a significant resource overhead. Recent advances have shown that by jointly decoding logical qubits in algorithms composed of transversal gates, the number of syndrome extraction rounds can be reduced by a factor of the code distance d, at the cost of increased classical decoding complexity. Here, we reformulate the problem of decoding transversal circuits by directly decoding relevant logical operator products as they propagate through the circuit. This procedure transforms the decoding task into one closely resembling that of a single-qubit memory propagating through time. The resulting approach leads to fast decoding and reduced problem size while maintaining high performance. Focusing on the surface code, we prove that this method enables fault-tolerant decoding with minimum-weight perfect matching, and benchmark its performance on example circuits including magic state distillation. We find that the threshold is comparable to that of a single-qubit memory, and that the total decoding run time can be, in fact, less than that of conventional lattice surgery. Our approach enables fast correlated decoding, providing a pathway to directly extend single-qubit QEC techniques to transversal algorithms.
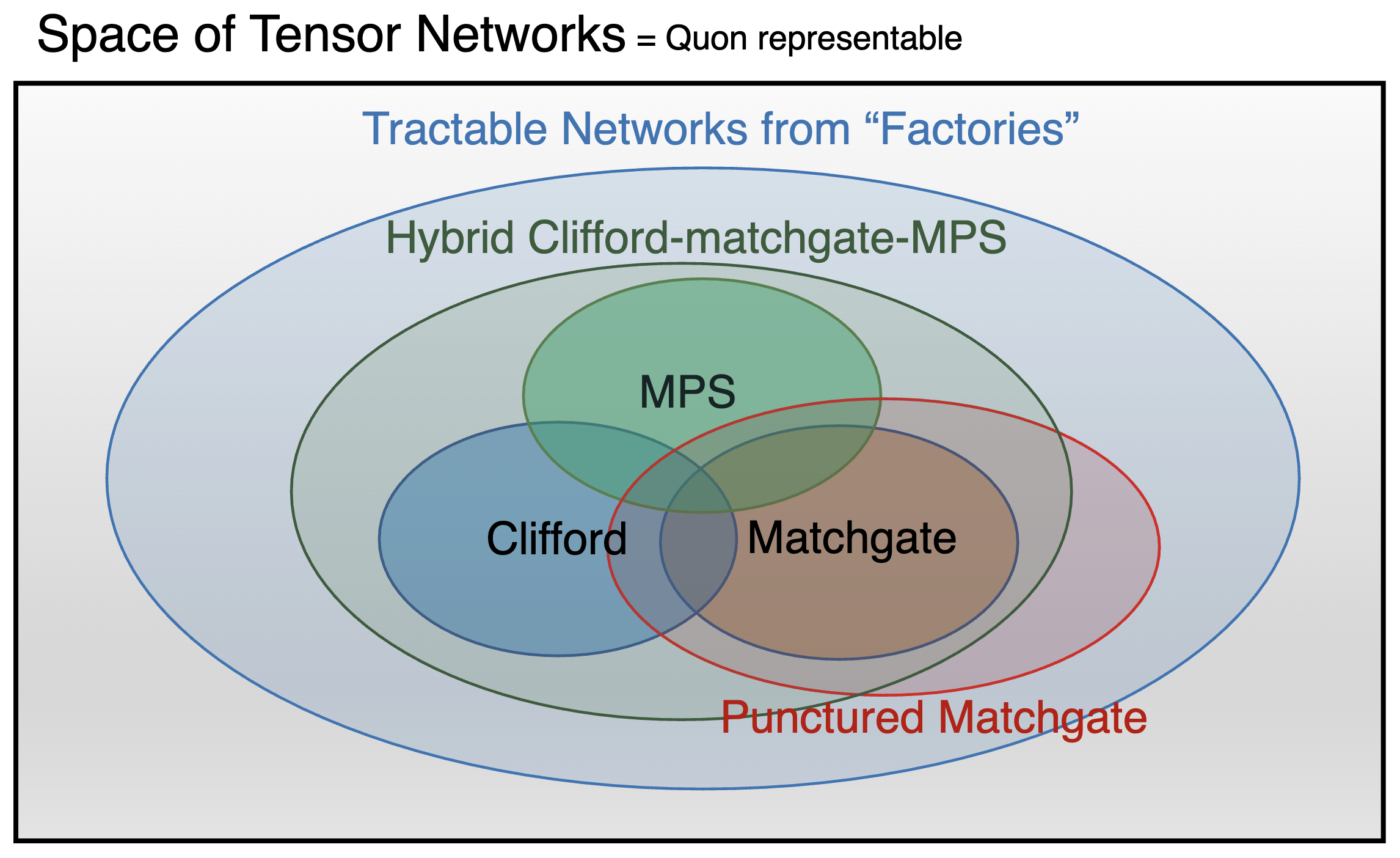
- 2D Quon Language: Unifying Framework for Cliffords, Matchgates, and Beyond
Abstract
Simulating generic quantum states and dynamics is practically intractable using classical computers. However, certain special classes—namely Clifford and matchgate circuits—permit efficient computation. They provide invaluable tools for studying many-body physics, quantum chemistry, and quantum computation. While both play foundational roles across multiple disciplines, the origins of their tractability seem disparate, and their relationship remain unclear. A deeper understanding of such tractable classes could expand their scope and enable a wide range of new applications. In this work, we make progress toward the unified understanding of the Clifford and matchgate—these two classes are, in fact, distinct special cases of a single underlying structure. Specifically, we introduce the 2D Quon language, which combines Majorana worldlines with their underlying spacetime topology to diagrammatically represent quantum processes and tensor networks. In full generality, the 2D Quon language is universal—capable of representing arbitrary quantum states, dynamics, or tensor networks—yet they become especially powerful in describing Clifford and matchgate classes. Each class can be efficiently characterized in a visually recognizable manner using the Quon framework. This capability naturally gives rise to several families of efficiently computable tensor networks introduced in this work: punctured matchgates, hybrid Clifford-matchgate-MPS, and ansatze generated from factories of tractable networks. All of these exhibit high non-Cliffordness, high non-matchgateness, and large bipartite entanglement entropy. We discuss a range of applications of our approach, from recovering well-known results such as the Kramers-Wannier duality and the star-triangle relation of the Ising model, to enabling variational optimization with novel ansatz states.
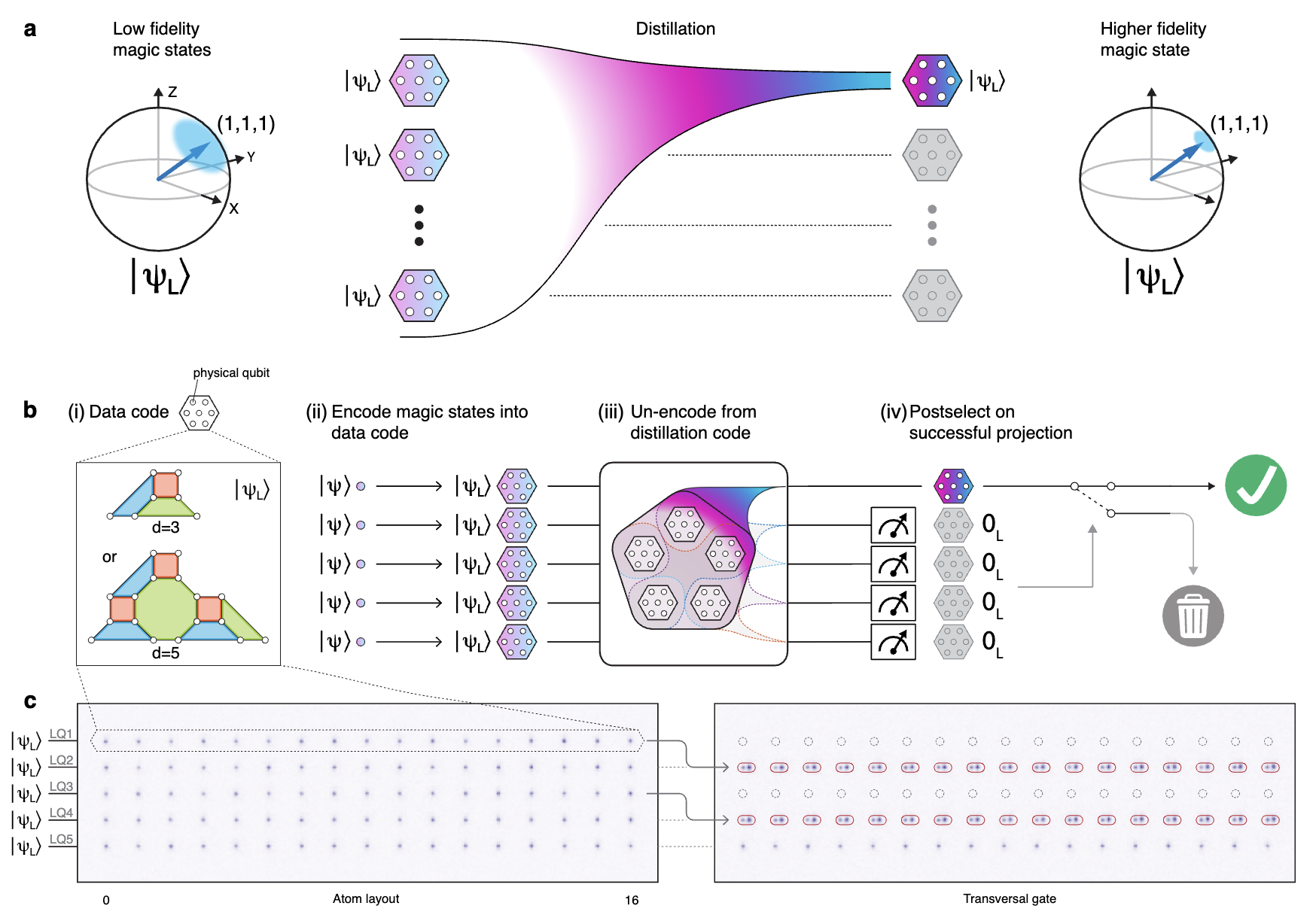
- Experimental Demonstration of Logical Magic State Distillation
Abstract
Realizing universal fault-tolerant quantum computation is a key goal in quantum information science. By encoding quantum information into logical qubits utilizing quantum error correcting codes, physical errors can be detected and corrected, enabling substantial reduction in logical error rates. However, the set of logical operations that can be easily implemented on such encoded qubits is often constrained, necessitating the use of special resource states known as 'magic states' to implement universal, classically hard circuits. A key method to prepare high-fidelity magic states is to perform 'distillation', creating them from multiple lower fidelity inputs. Here we present the experimental realization of magic state distillation with logical qubits on a neutral-atom quantum computer. Our approach makes use of a dynamically reconfigurable architecture to encode and perform quantum operations on many logical qubits in parallel. We demonstrate the distillation of magic states encoded in d=3 and d=5 color codes, observing improvements of the logical fidelity of the output magic states compared to the input logical magic states. These experiments demonstrate a key building block of universal fault-tolerant quantum computation, and represent an important step towards large-scale logical quantum processors.
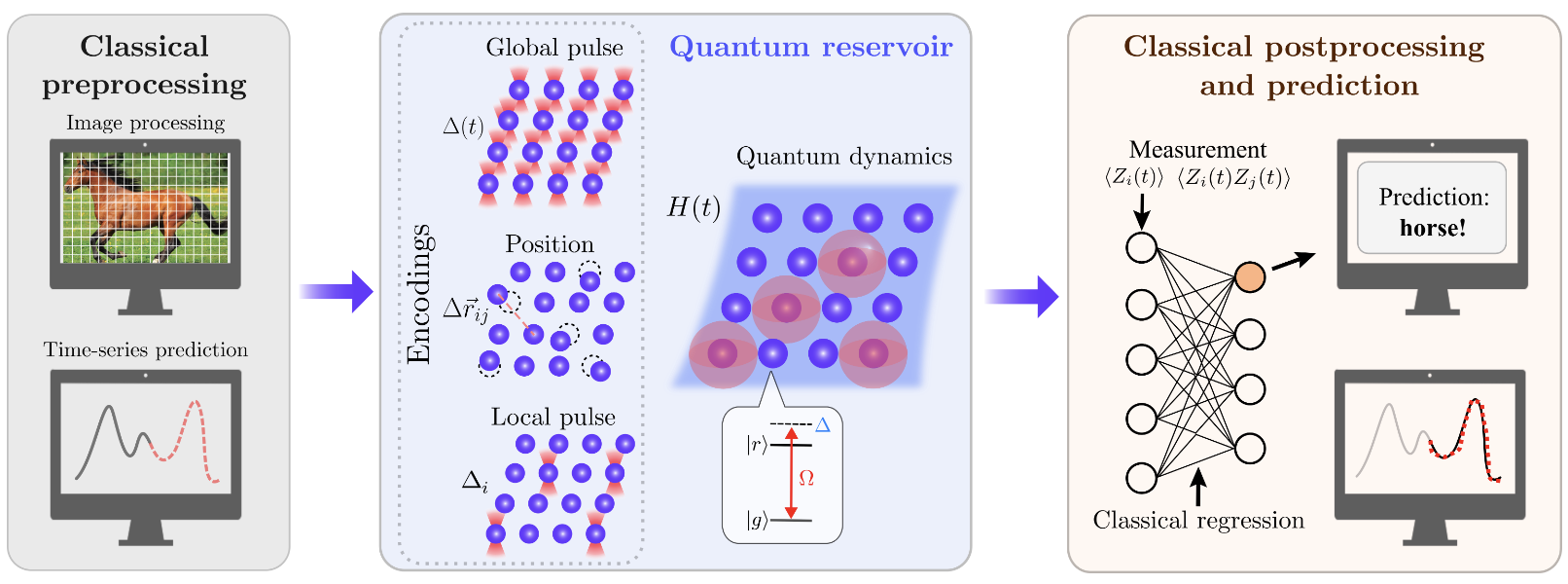
InNature - Large-scale quantum reservoir learning with an analog quantum computer
Abstract
Quantum machine learning has gained considerable attention as quantum technology advances, presenting a promising approach for efficiently learning complex data patterns. Despite this promise, most contemporary quantum methods require significant resources for variational parameter optimization and face issues with vanishing gradients, leading to experiments that are either limited in scale or lack potential for quantum advantage. To address this, we develop a general-purpose, gradient-free, and scalable quantum reservoir learning algorithm that harnesses the quantum dynamics of neutral-atom analog quantum computers to process data. We experimentally implement the algorithm, achieving competitive performance across various categories of machine learning tasks, including binary and multi-class classification, as well as timeseries prediction. Effective and improving learning is observed with increasing system sizes of up to 108 qubits, demonstrating the largest quantum machine learning experiment to date. We further observe comparative quantum kernel advantage in learning tasks by constructing synthetic datasets based on the geometric differences between generated quantum and classical data kernels. Our findings demonstrate the potential of utilizing classically intractable quantum correlations for effective machine learning. We expect these results to stimulate further extensions to different quantum hardware and machine learning paradigms, including early fault-tolerant hardware and generative machine learning tasks.
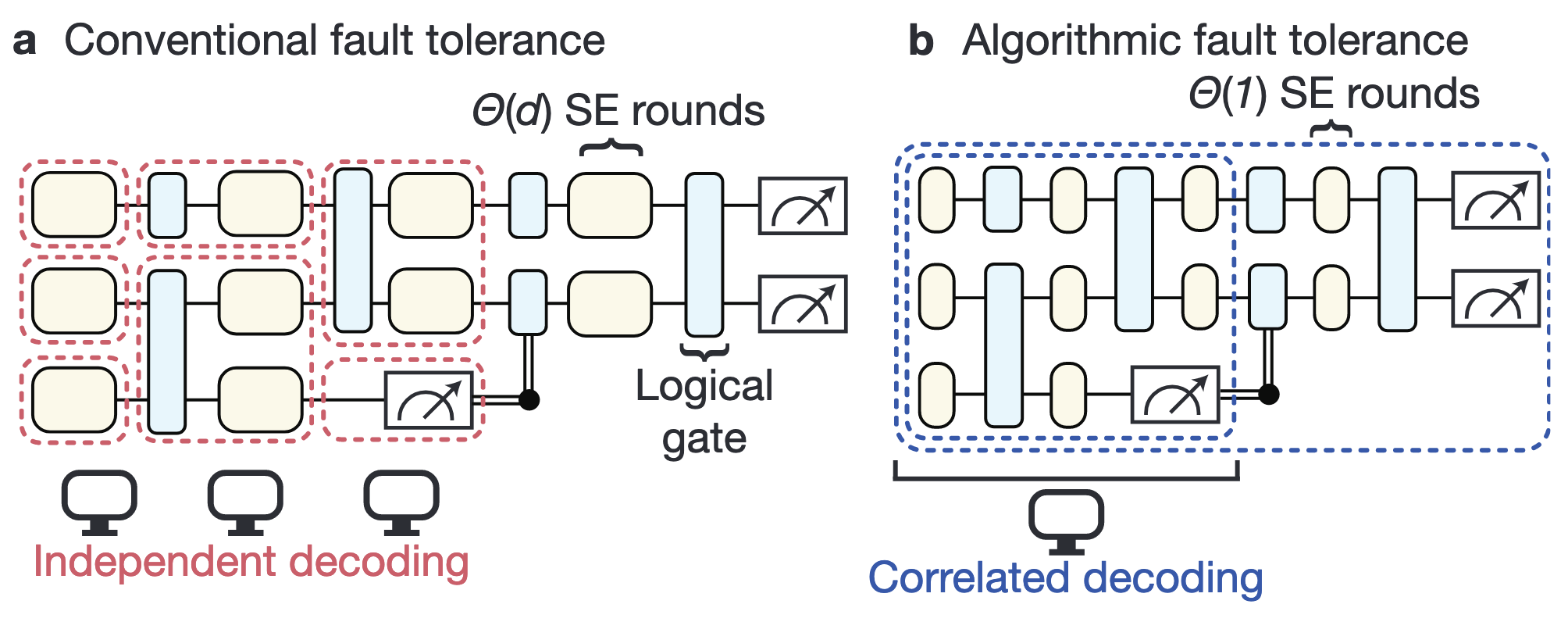
- Low-overhead transversal fault tolerance for universal quantum computation
Abstract
Fast, reliable logical operations are essential for realizing useful quantum computers. By redundantly encoding logical qubits into many physical qubits and using syndrome measurements to detect and correct errors, we can achieve low logical error rates. However, for many practical quantum error correction codes such as the surface code, owing to syndrome measurement errors, standard constructions require multiple extraction rounds—of the order of the code distance d—for fault-tolerant computation, particularly considering fault-tolerant state preparation. Here we show that logical operations can be performed fault-tolerantly with only a constant number of extraction rounds for a broad class of quantum error correction codes, including the surface code with magic state inputs and feedforward, to achieve ‘transversal algorithmic fault tolerance’. Through the combination of transversal operations and new strategies for correlated decoding13, despite only having access to partial syndrome information, we prove that the deviation from the ideal logical measurement distribution can be made exponentially small in the distance, even if the instantaneous quantum state cannot be made close to a logical codeword because of measurement errors. We supplement this proof with circuit-level simulations in a range of relevant settings, demonstrating the fault tolerance and competitive performance of our approach. Our work sheds new light on the theory of quantum fault tolerance and has the potential to reduce the space–time cost of practical fault-tolerant quantum computation by over an order of magnitude.
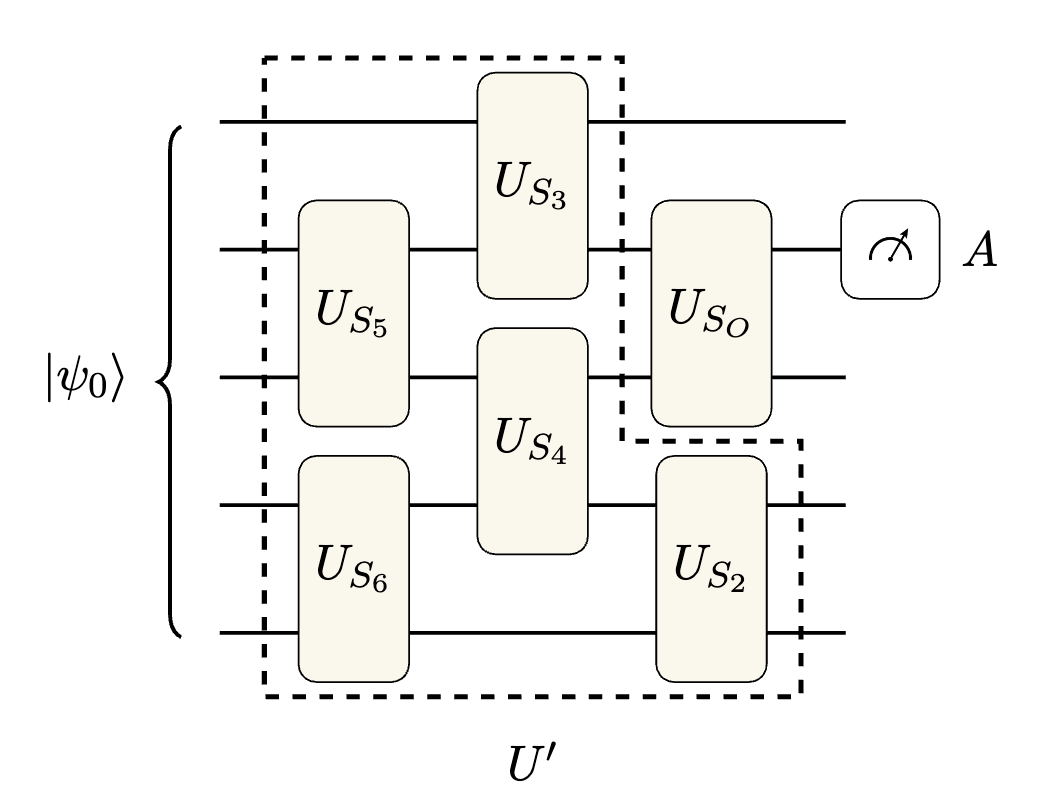
InNature - Correlated decoding of logical algorithms with transversal gates
Abstract
Quantum error correction is believed to be essential for scalable quantum computation, but its implementation is challenging due to its considerable space-time overhead. Motivated by recent experiments demonstrating efficient manipulation of logical qubits using transversal gates [Bluvstein et al., Nature (London) 626, 58 (2024)], we show that the performance of logical algorithms can be substantially improved by decoding the qubits jointly to account for error propagation during transversal entangling gates. We find that such correlated decoding improves the performance of both Clifford and non-Clifford transversal entangling gates, and explore two decoders offering different computational runtimes and accuracies. In particular, by leveraging the deterministic propagation of stabilizer measurement errors, we find that correlated decoding enables the number of noisy syndrome extraction rounds between gates to be reduced from O(d) to O(1) in transversal Clifford circuits, where 𝑑 is the code distance. We verify numerically that this approach substantially reduces the space-time cost of deep logical Clifford circuits. These results demonstrate that correlated decoding provides a major advantage in early fault-tolerant computation, as realized in recent experiments, and further indicate it has considerable potential to reduce the space-time cost in large-scale logical algorithms.
InPhysical Review Letters - Barren plateaus from learning scramblers with local cost functions
Abstract
The existence of barren plateaus has recently revealed new training challenges in quantum machine learning (QML). Uncovering the mechanisms behind barren plateaus is essential in understanding the scope of problems that QML can efficiently tackle. Barren plateaus have recently been shown to exist when learning global properties of random unitaries, which is relevant when learning black hole dynamics. Establishing whether local cost functions can circumvent these barren plateaus is pertinent if we hope to apply QML to quantum many-body systems. We prove a no-go theorem showing that local cost functions encounter barren plateaus in learning random unitary properties.
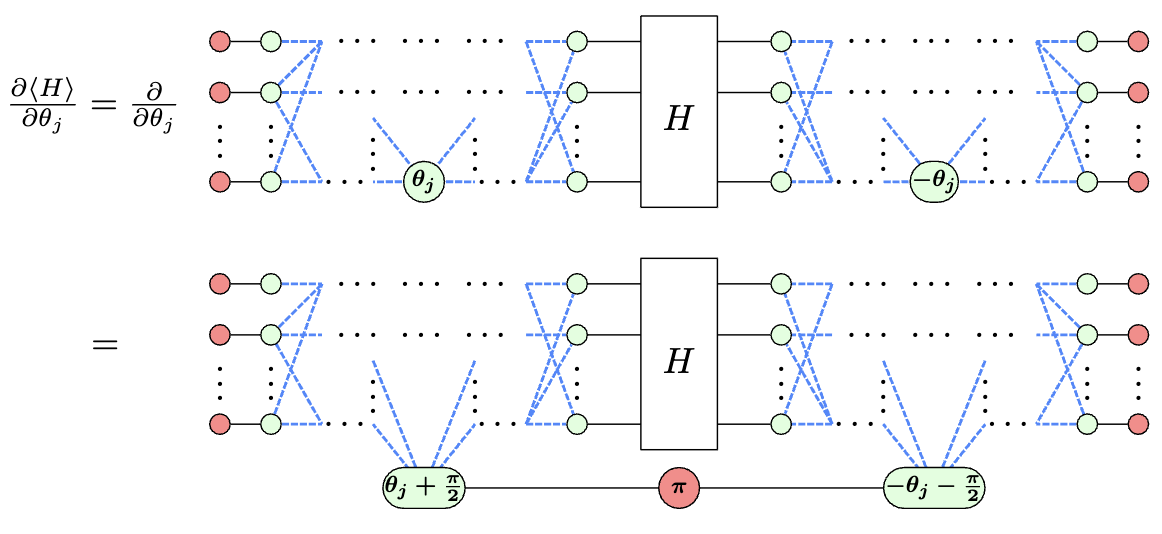
InJournal of High Energy Physics - Analyzing the barren plateau phenomenon in training quantum neural networks with the ZX-calculus
Abstract
In this paper, we propose a general scheme to analyze the gradient vanishing phenomenon, also known as the barren plateau phenomenon, in training quantum neural networks with the ZX-calculus. More precisely, we extend the barren plateaus theorem from unitary 2-design circuits to any parameterized quantum circuits under certain reasonable assumptions. The main technical contribution of this paper is representing certain integrations as ZX-diagrams and computing them with the ZX-calculus. The method is used to analyze four concrete quantum neural networks with different structures. It is shown that, for the hardware efficient ansatz and the MPS-inspired ansatz, there exist barren plateaus, while for the QCNN ansatz and the tree tensor network ansatz, there exists no barren plateau.
InQuantum